Nhiều người cho rằng hàm tài chính chỉ dùng trong các nghiệp vụ tài chính, ngân hàng. Nhưng thực tế, một số hàm sẽ có ích cho tất cả chúng ta, nhất là những ai muốn vay vốn mua nhà, gửi tiết kiệm ngân hàng. Bởi chúng giúp tính giá trị thời gian của tiền, tính lãi của khoản vay, tính lãi thực của khoản vay trả góp… Trong bài viết này, Kiến thức kinh tế sẽ cùng bạn tìm hiểu, nắm rõ các hàm tài chính đó. 

Hàm tài chính FV 

Trong các hàm tài chính cơ bản, hàm FV được dùng để xác định tổng số tiền mà bạn nhận được khi gửi một số tiền nhất định vào một ngân hàng có lãi suất nhất định.

Cú pháp: = FV(rate, nper, pmt, pv, type)

Trong đó:

- rate: là lãi suất nhưng phải nói rõ là lãi suất quy đổi theo kỳ gửi tiền. Nếu kỳ là 1 tháng, rate phải tính cho tháng, kỳ là quý, rate phải tính cho quý 3 tháng.

- nper là số kỳ gửi tiền không phải là tổng thời gian gửi. Tổng thời gian gửi tính theo đơn vị gì? Trong khi kỳ có thể là tuần, là tháng, là quý, là năm.

- pmt là là số tiền gửi hàng tháng bằng nhau trong nper kỳ

- pv là giá trị hiện tại (present value). Ý nghĩa của [pv] trong hàm là số tiền có sẵn trong ngân hàng vào thời điểm bạn gửi. Mặc định nếu bỏ qua tham số này nghĩa là số tiền ban đầu bằng không.

Ví dụ:

Bạn muốn gửi số tiền là 10.000 USD (định kỳ hàng tháng) vào ngân hàng A, với lãi suất là 5% /năm, trong thời gian 10 năm. Số dư tiền gửi có sẵn trong TK ngân hàng là 25.000 USD.

Như vậy:

Tổng số tiền mà bạn nhận được sau 10 năm sẽ được tính theo hàm FV(rate, nper, pmt, pv, type). 

- 10.000 USD là số tiền gửi hàng tháng bằng nhau trong nper kỳ, và 10.000 USD là tham số pmt trong hàm.

- pv là tiền có sẵn trong tài khoản trước khi bạn gửi 10.000 USD. Ở đây thì pv = 25.000 USD.

- nper = 10 năm.

- rate = 5% tương ứng với nper theo năm.

Kết quả, số tiền nhận được trong tương lai gồm cả gốc và lãi của TK tiền gửi là: 172.790USD

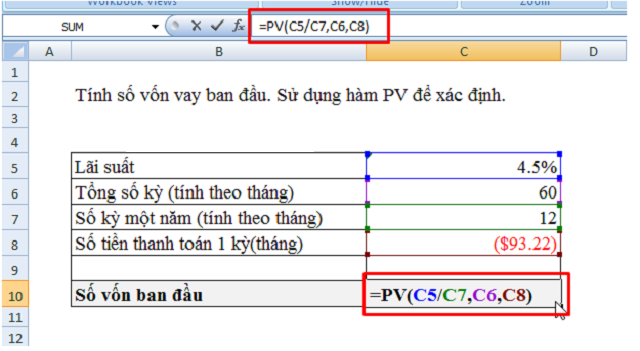
Ví dụ về hàm tài chính PV

>>> Bài viết được quan tâm: Cách tính lãi ngân hàng đơn giản nhất

Hàm tài chính PMT 

Hàm PMT có chức năng ngược với FV, đó là khi bạn đã biết trước: số tiền nhận được, thời gian gửi tiền và lãi suất ngân hàng. Lúc đó, dùng hàm PMT sẽ giúp bạn tính được tổng số tiền bạn cần phải gửi vào là bao nhiêu.

Cụ thểm, hàm PMT giúp:

Tính số tiền cố định và phải trả định kỳ đối với một khoản vay có lãi suất không đổi.

Cũng có thể dùng hàm này để tính số tiền cần đầu tư định kỳ (gửi tiết kiệm, chơi bảo hiểm..) để cuối cùng sẽ có một khoản tiền nào đó.

Cú pháp: = PMT(rate, nper, pv, fv, type)

Trong đó:  

- Rate : Lãi suất của mỗi kỳ (tính theo năm). Nếu trả lãi hằng tháng thì bạn chia lãi suất cho 12.

Ví dụ, nếu bạn kiếm được một khoản vay với lãi suất 10% mỗi năm, trả lãi hằng tháng, thì lãi suất hằng tháng sẽ là 10%/12, hay 0.83%; bạn có thể nhập 10%/12, hay 0.83%, hay 0.0083 vào công thức để làm giá trị cho rate.

- Nper : Tổng số kỳ phải trả lãi (tính theo năm). Nếu số kỳ trả lãi là hằng tháng, bạn phải nhân nó với 12.

Ví dụ, bạn mua một cái xe với khoản trả góp 4 năm và phải trả lãi hằng tháng, thì số kỳ trả lãi sẽ là 4*12 = 48 kỳ; bạn có thể nhập 48 vào công thức để làm giá trị cho nper.

- Pv: Giá trị hiện tại (hiện giá), hoặc là tổng giá trị tương đương với một chuỗi các khoản phải trả trong tương lai; cũng có thể xem như số vốn ban đầu (xem thêm hàm PV)

- Fv: Giá trị tương lai. Với một khoản vay, thì nó là số tiền nợ gốc còn lại sau lần trả lãi sau cùng; nếu là một khoản đầu tư, thì nó là số tiền sẽ có được khi đáo hạn. Nếu bỏ qua fv, trị mặc định của fv sẽ là zero (0) (xem thêm hàm FV)

- Type : Hình thức chi trả:

= 0 : Chi trả vào cuối mỗi kỳ (mặc định)

= 1 : Chi trả vào đầu mỗi kỳ tiếp theo

Lưu ý:

Rate và nper phải sử dụng đơn vị tính toán nhất quán với nhau. Ví dụ: Với khoản vay trong 4 năm, lãi suất hằng năm là 10%, nếu chi trả hằng tháng thì dùng 10%/12 cho rate và 4*12 cho nper; còn nếu chi trả hằng năm thì dùng 10% cho rate và 4 cho nper.

Kết quả (số tiền) do hàm PMT trả về bao gồm tiền gốc và tiền lãi, nhưng không bao gồm thuế và những khoản lệ phí khác (nếu có).

Nếu muốn chỉ tính số tiền gốc phải trả, ta dùng hàm PPMT, còn nếu muốn chỉ tính số tiền lãi phải trả, dùng làm IPMT.

Ví dụ:

Bạn mua trả góp một căn hộ với giá $1,000,000,000, trả góp trong 30 năm, với lãi suất không đổi là 8% một năm trong suốt thời gian này, vậy mỗi tháng bạn phải trả cho người bán bao nhiêu tiền để sau 30 năm thì căn hộ đó thuộc về quyền sở hữu của bạn ?

= PMT(8%/12, 30*12, 1000000000) = $7,337,645/74

Ở công thức trên, đối số fv = 0, là do sau khi đã thanh toán xong khoản tiền cuối cùng, thì bạn không còn nợ nữa.

Nhưng khi nhẩm lại, ta sẽ thấy mua trả góp.. thành mua đắt gấp hơn 2 lần!

Bạn muốn có một số tiền tiết kiệm là $50,000,000 sau 10 năm, biết rằng lãi suất (không đổi) của ngân hàng là 12% một năm, vậy từ bây giờ, hằng tháng bạn phải gửi vào ngân hàng bao nhiêu tiền ?

= PMT(12%/12, 10*12, 0, 50000000) = $217,354.74

Ở công thức trên, đối số pv = 0, là do ngay từ đầu, bạn không có đồng nào trong ngân hàng cả.

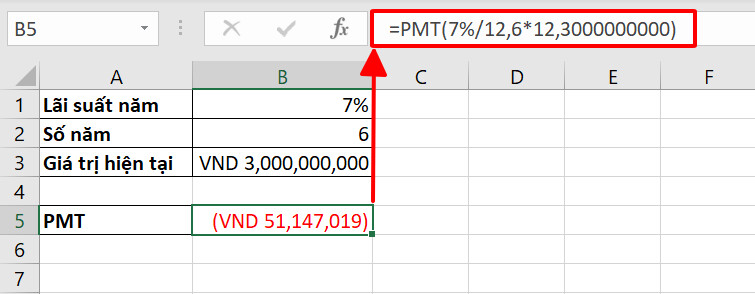
Ví dụ về hàm tài chính PMT

Hàm tài chính RATE

Hàm RATE dùng để tính lãi suất của mỗi kỳ trong một niên kim (annuity), hay là tính lãi suất của mỗi kỳ của một khoản vay.

RATE được tính bởi phép lặp và có thể có một hay nhiều kết quả. Nếu các kết quả của RATE không thể hội tụ vào trong 0.0000001 sau 20 lần lặp, RATE sẽ trả về giá trị lỗi #VALUE!

Cú pháp: = RATE(nper, pmt, pv, fv, type, guess)

Trong đó:

- Nper: Tổng số kỳ phải trả lãi (tính theo năm). Nếu số kỳ trả lãi là hằng tháng, bạn phải nhân nó với 12.

Ví dụ, bạn mua một cái xe với khoản trả góp 4 năm và phải trả lãi hằng tháng, thì số kỳ trả lãi sẽ là 4*12 = 48 kỳ; bạn có thể nhập 48 vào công thức để làm giá trị cho nper.

- Pmt : Số tiền phải trả trong mỗi kỳ. Số tiền này sẽ không thay đổi trong suốt năm.Pmt bao gồm cả tiền gốc và tiền lãi (không bao gồm lệ phí và thuế). Ví dụ, số tiền phải trả hằng tháng là $10,000 cho khoản vay mua xe trong 4 năm với lãi suất 12% một năm là $263.33; bạn có thể nhập -263.33 vào công thức làm giá trị cho pmt.

Nếu bỏ qua pmt thì bắt buộc phải có fv.

- Pv : Giá trị hiện tại (hiện giá), hoặc là tổng giá trị tương đương với một chuỗi các khoản phải trả trong tương lai.

- Fv : Giá trị tương lai. Với một khoản vay, thì nó là số tiền nợ gốc còn lại sau lần trả lãi sau cùng; nếu là một khoản đầu tư, thì nó là số tiền sẽ có được khi đáo hạn. Nếu bỏ qua fv, trị mặc định của fv sẽ là zero (ví dụ, sau khi bạn đã thanh toán hết khoản vay thì số nợ của bạn sẽ bằng 0).

- Type : Hình thức tính lãi:

= 0 : Tính lãi vào cuối mỗi kỳ (mặc định)

= 1 : Tính lãi vào đầu mỗi kỳ tiếp theo

Guess : Giá trị của lãi suất hằng năm (rate), do bạn dự đoán. Nếu bỏ qua, Excel sẽ mặc định cho guess = 10%.

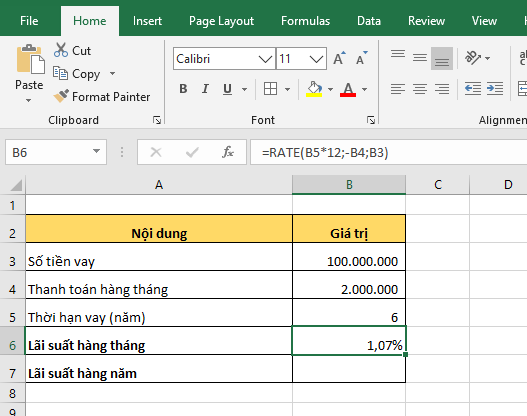
Ví dụ về hàm tài chính RATE

Lưu ý:

Nếu RATE() báo lỗi #VALUE! (do không hội tụ), hãy thử với các giá trị khác cho guess.

Nper và Guess phải sử dụng đơn vị tính toán nhất quán với nhau. Ví dụ: Với khoản vay trong 4 năm, lãi suất hằng năm là 10%, nếu chi trả hằng tháng thì dùng 10%/12 choguess và 4*12 cho nper; còn nếu chi trả hằng năm thì dùng 10% cho guess và 4 chonper.

Ví dụ:

Giả sử bạn muốn vay trả góp $8,000,000 trong 4 năm, nhân viên ngân hàng sau một hồi tính toán, phán rằng mỗi tháng bạn phải trả cả gốc lẫn lãi là $200,000. Vậy ngân hàng đó tính lãi suất hằng tháng (hoặc lãi suất hằng năm) cho bạn là bao nhiêu ?

Lãi suất hằng tháng (dự đoán lãi suất là 10%/năm):

= RATE(4*12, -200000, 8000000) = 1%

Lãi suất hằng năm (dự đoán lãi suất là 10%/năm):

= RATE(4*12, -200000, 8000000)*12 = 9.24%

· Tính lãi suất mỗi năm cho một khoản vay $1,000 trong 2 năm, mỗi năm phải trả $100, khi đáo hạn phải trả cả gốc lẫn lãi là $1,200 ?

= RATE(2, -100, 1000, -1200) = 19%

Tựu trung lại, những hàm tài chính cơ bản này không chỉ có ích đối với nhân viên ngành ngân hàng, tài chính mà còn có ý nghĩa đối với nhiều người, nhất là với những ai có kế hoạch vay ngân hàng. Các hàm tài chính trong exel không hề khó học, cách học tốt nhất là bạn nên tổng hợp các dạng bài tập hàm tài chính và thực hành trên máy tính mỗi ngày. Chúc bạn thành công! 

>>> Xem thêm: TOP 26 sách kinh tế hay xuất sắc